Tensile tester

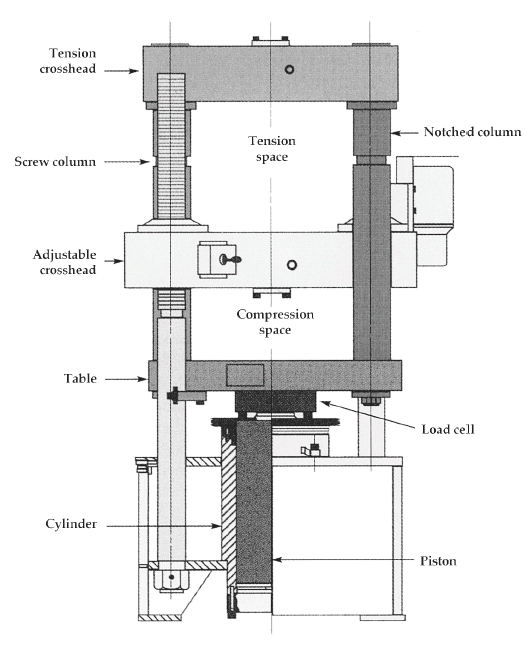
In a tensile tester a specimen of the polymer to be tested is stretched until it breaks. The test is usually done at room temperature. During this test the deformation of the specimen and the force used for the extension are measured. The speed of the deformation (or strain rate) is normally kept constant. An example of a stress-strain diagram thus obtained from PVC is shown in the figure. The actual stress in the specimen is calculated by dividing the measured force by the surface of the specimen.

At the start of the test, when the deformation is still small, the stress first rises fast until a maximum has been reached. This maximum is called the yield stress. On further deformation, the measured stress reduces some 10 to 20 % and then rises again.

The yield stress gives an indication of the strength of the polymer. As long as the stress is below the yield stress then the polymer behaves like an elastic solid. Close to the yield stress however the polymer starts to deform plastically.

The tensile test can be done at different strain rates of the specimen. It is commonly observed that the yield stress increases logarithmically with the strain rate.

What makes a polymer yield?

In the glass phase the Kuhn segment rotation time is very long. When a small stress is applied the polymer chains can only bend a little. This gives the polymer a stiff behaviour.

However, things change when the stress becomes high enough. We have seen in chapter 7 that the stress strongly reduces the rotation time of the Kuhn segments. When the stress has reached the yield stress the rotation time has reduced to a few seconds. That is low enough to make the plastic deform on a human time scale. It now behaves rubbery.

How to calculate the yield stress from the differential equation

In chapter 8 we have shown the general outline of the differential equation for the glass phase:
[change of glass stress per unit of time] = + [change of glass stress due to deformation per unit of time] – [glass stress] / [glass relaxation time]

This differential equation can be used for the calculation of the yield stress from the material properties. At the moment of yield the stress does not change anymore. It is constant and equal to the yield stress. That means that the change of glass stress per unit of time is zero. Now the differential equation looks as follows:
0 = + [change of glass stress due to deformation per unit of time] – [yield stress] / [glass relaxation time]

In case of small deformations, which is the case before yielding, the stress is proportional to the deformation. The proportionality factor is the Young’s modulus:
[glass stress] = [Young’s modulus] * [deformation]

It then follows that the change of glass stress per unit of time is equal to the Young’s modulus times the deformation speed:
[change of glass stress due to deformation per unit of time] = [Young’s modulus] * [deformation speed]

We can rewrite this equation to determine the glass stress under those particular circumstances:
[yield stress] = [Young’s modulus] * [glass relaxation time] * [deformation speed]

The yield stress is now found by applying the actual material properties into the equation above.

Summary

• The strength of a polymer is tested with a tensile tester.
• At a certain stress the polymer suddenly starts to deform plastically. This stress is called the yield stress.
• Yielding is caused by the stress-accelerated rotation of the Kuhn segments. At the yield stress the rotation speed of the Kuhn segments is high enough to follow the applied deformation speed.
• The yield stress can be determined from the differential equation for the glass stress relaxation. At the moment of yield the stress does not change anymore and there exists a dynamic equilibrium.

Learn more: